Look up most references to Zernike polynomials and you will quickly discover there are multiple methods for ordering the polynomials. This page provides historical context for the Fringe ordering as specified in the FRINGE Manual, version 3 (1982). As one of the first programs for working with Zernike polynomials, the FRINGE software had significant impact in optical design and analysis.

The original code was largely created by John S. Loomis at the Optical Sciences Center in the University of Arizona. If anyone has information about earlier versions of this manual or the code, please contact me.

Zernike Ordering
Ordering used in the FRINGE software defies modern conventions by ignoring the constant term, often referred to as piston (Z00). Spread over 3 pages, the ordering of the 36 terms defined in the manual are shown below.



Over the years, the missing piston term has either been added as a 0th element, or listed as the first element with all the subsequent indices increased by one. It is likely beyond hope to settle on a consistent numbering scheme.
Historical Notes
Table of Contents
This manual is impressive for its scope. Containing over 230 pages with appendices, it provides detailed information about program usage, inputs, outputs, and related reference material that is useful when working with Zernike polynomials.


Art work
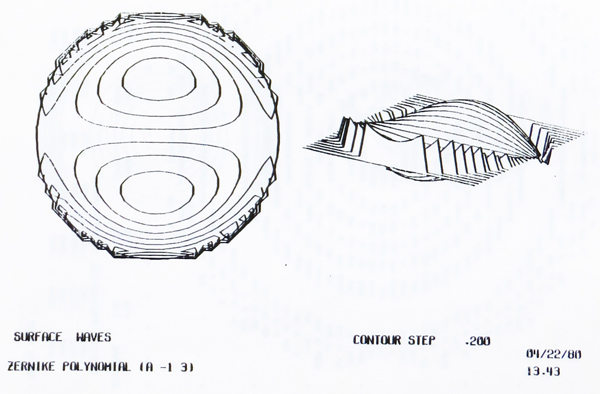
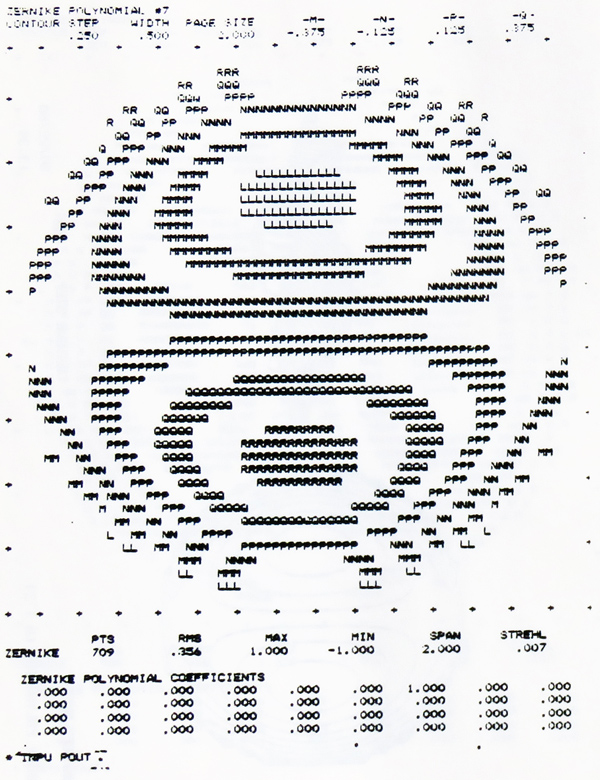
Even more impressive than the manual, was the program itself. Using a combination of ASCII art and line drawings, the FRINGE software was able to generate beautiful images and 3D plots of Zernike surfaces.
Note to User
Perhaps best of all, the FRINGE software was able to do all this while fitting in 68 kB of memory.